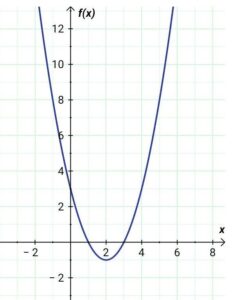
Diketahui:suatu fungsi f (x) = x²-4x+3
tentukan:
• titik Potong terhadap sumbu x !
• titik Potong terhadap sumbu y!
• Diskriminan Fungsi tersebut !
• Sumbu Simetri Fungsi tersebut !
• Nilai optimun /minimum
• Titik Puncak fungsi tersebut !
• gambarlah Grafik fungsi tersebut !
Jawaban
f(x) = x²-4x+3
a = 1, b = -4, c = 3
• titik Potong terhadap sumbu x, y = 0
x² – 4x + 3 = 0
(x – 1)(x – 3) = 0
x – 1 = 0 atau x – 3 = 0
x = 1 x = 3
maka titik potongnya (1, 0) dan (3, 0)
• titik Potong terhadap sumbu y!
titiknya (0, c) = (0, 3)
• Diskriminan Fungsi tersebut !
D = b² – 4ac
= (-4)² – 4.1.3
= 16 – 12
= 4
• Sumbu Simetri Fungsi tersebut !
x = -b/2a
= -(-4)/2.1
= 4/2
= 2
• Nilai optimun /minimum
f(2) = 2² – 4.2 + 3
= 4 – 8 + 3
= -1
• Titik Puncak fungsi tersebut !
(2, -1)
• gambarlah Grafik fungsi tersebut !
terlampir
Daftar isi
 IlmuanTekno Berita tentang Gadget, Teknologi, Trading, Forex, Saham, Investasi, Bisnis, dan Info Keuangan.
IlmuanTekno Berita tentang Gadget, Teknologi, Trading, Forex, Saham, Investasi, Bisnis, dan Info Keuangan.