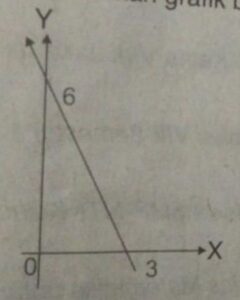Perhatikan grafik berikut! Berapakah gradien garis tersebut?
jawaban untuk soal ini adalah gradien garis tersebut.
Soal diatas merupakan materi persamaan garis lurus. Gradien adalah nilai yang menunjukkan kemiringan/kecondongan suatu garis lurus.
Ingat!
Diketahui,
Ditanyakan,
Dijawab,
Sehingga dapat disimpulkan bahwa, gradien garis tersebut adalah – 2.
Rekomendasi lainnya : Persamaan garis berikut yang sejajar dengan x-3y=6… Persamaan garis berikut yang sejajar dengan x-3y=6 adalah .... A. 2x-6y=5 B. 3x-y=6 C. 6x + 2y = 9 D. x + 3y = 6… Tentukan gradien garis singgung pada kurva x=x²-6x+9… tentukan gradien garis singgung pada kurva x=x²-6x+9 dititik (1,4) Jawaban yang benar adalah m = -4 Perhatikan beberapa aturan turunan fungsi berikut: > Jika f(x)… Persamaan garis yang melalui titik (3, –4) dan tegak… Persamaan garis yang melalui titik (3, –4) dan tegak lurus dengan garis yang memiliki gradien ½ adalah jawaban untuk soal ini adalah y = -… Gambarlah grafik yang menunjukkan persamaan garis… Gambarlah grafik yang menunjukkan persamaan garis lurus 2x-5y-9=0! Jawabannya: terdapat pada gambar di bawah Dalam membuat grafik kita perlu menentukan titik yang memotong di sumbu… Tentukan persamaan garis yang sejajar garis y=x+10… Tentukan persamaan garis yang sejajar garis y=x+10 dan melalui titik p (-1.2) Jawaban : y = x + 3 Ingat! Rumus mencari persamaan garis yang… Gradien garis singgung kurva y=x²+2x+1 pada titik… Gradien garis singgung kurva y=x²+2x+1 pada titik berabsis 1 sama dengan ... a. 1 b. 2 c. 3 d. 4 e. 5 Ingat! "Jika y… Tentukan gradien garis: 2x−3y+6=0 Tentukan gradien garis: 2x−3y+6=0 Jawaban dari pertanyaan di atas adalah 2/3. Perhatikan konsep berikut. Gradien dari persamaan garis ax + by + c = 0… Jika garis m menyinggung kurva dengan persamaan y =… Jika garis m menyinggung kurva dengan persamaan y = x3^ + 6x2^ -10di titik (1,-3) maka persamaan garis m adalah.... Jawaban yang benar adalah y… Persamaan garis melalui titik (-1, 2) dan sejajar… 19. Persamaan garis melalui titik (-1, 2) dan sejajar dengan garis y= -2/3x+6 adalah.... A. 2x + 3y = -8 B. 2x + 3y =… Persamaan garis yang melalui (2,−1) bergradien 3/4 adalah … Persamaan garis yang melalui (2,−1) bergradien 3/4 adalah … A. 3x−4y−2=0 B. 3x−4y−10=0 C. 3x+4y−2=0 D. 3x+4y+10=0 Jawaban dari pertanyaan di atas adalah B. Perhatikan… Tentukan gradien garis yang melalui titik pusat O… Tentukan gradien garis yang melalui titik pusat O dan titik P(3,9). Jawaban dari pertanyaan di atas adalah 3. Perhatikan konsep berikut. Misalkan terdapat garis yang… Tentukan persamaan garis dengan m=16x+3 melalui titik (0,5) tentukan persamaan garis dengan m=16x+3 melalui titik (0,5) Jawaban: y = 3x + 5. Konsep: Rumus persamaan garis dengan gradien m dan melalui (x1, y1)… Gradien garis singgung kurva y=x²–6x+9 di titik (1,… Gradien garis singgung kurva y=x²–6x+9 di titik (1, 4) sama dengan ... a. –4 b. –3 c. –1 d. 5 e. 8 turunan pertama =… Posisi garis yang melalui Zulfa dan Zulfi adalah .... Posisi garis yang melalui Zulfa dan Zulfi adalah .... A. berimpit dengan sumbu x B. sejajar dengan sumbu y C. tegak lurus dengan sumbu x… Diketahui persamaan kurva y = x² - 5x , tentukan… diketahui persamaan kurva y = x² - 5x , tentukan persamaan garis singgung pada kurva titik yg berbabsis 2 Pertama cari nilai y dengan memasukkan…
 IlmuanTekno Berita tentang Gadget, Teknologi, Trading, Forex, Saham, Investasi, Bisnis, dan Info Keuangan.
IlmuanTekno Berita tentang Gadget, Teknologi, Trading, Forex, Saham, Investasi, Bisnis, dan Info Keuangan.